The first part of the course will be devoted to Hilbert’s 16th problem for algebraic curves, which was one of the starting points for the real algebraic geometry. Given a smooth real algebraic plane curve of a given degree, how many components could it have? How many of them may be nested in the other ones?
Hilbert himself resolved the problem up to degree 6 modulo one elusive topological type, whose existence was proved only 70 years later. Our aim is Viro’s patchworking theorem, which allows to construct algebraic curves of a given degree with prescribed topology. For example, here is the patchworking construction for the aforementioned elusive curve:
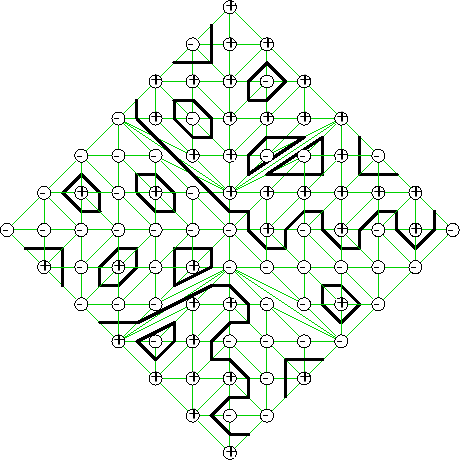
The second part of the course will be devoted to toric varieties. We first enocunter them when proving the patchworking theorem, and they have many other applications accross various parts of geometry. Toric varieties are certain algebraic varieties that can be assigned to lattice polytopes. This correspondence between algebraic and polyhedral objects turns out to be extremely profitable for both fields of study. For instance, on the polyhedral side, it resolves the Upper bound conjecture on the number of faces of a simple polytope, and, on the side of algebric geometry, it leads to the theory of Newton polytopes.